Jimmy Ta - Model Mutations

Hexcripting Landscapes

In Hexcripting Landscapes, landscape form finding explores the python scripting as effective and precise modeling. Scripting in landscape modeling allows full control to generate landscapes and produce numerous design iterations. The project explores topology and land form finding. As a result, the models produce bizarre unconventional alien landscapes, but allow the exploration of form finding and design testing.

Through exploration of design form finding, generative design provides the efficiency of creating the tools as a template to limit remodeling, to quantify design performance, and to generate precise modeling. Generative design limit remodeling by providing pre-made tools by the user to recreate the series of steps, thus saving time by having the computer to reprocess pre-made design tools. Furthermore, pre-made design tools limit the amount of human errors made and quantify numbers as results to determine performances.

Devil’s postpile exhibits geometric forms created by volcanic activities. Dissecting the geometric forms of the Devil’s Postpile, the landform resembles the series of steps from geometric shape to line to extrusion forms. These forms are taken to be studied as a way of determining how to create landscapes in a scripting methology. The methology provides a clear understanding of how to provide a instruction to replicate the existing landscapes. Devil’s Postpile is provided as a case study to move to generate the first steps of an alien landscape.

Giant’s Causaway, located in Northern Ireland, is also a natural wonder and is formed by volcanic activities as well. These formations exhibit the geometric forms and provide a case study of studying the forms to dissect the series of steps to script a digital model to exercise the scripting of natural landscapes. While studying these landscapes, the form finding and geometric studies provide the step by step instructions to recreate the form language.

While Devil’s Postpile and Giant’s Causaway provide a case study from the existing landscape, these existing sites provide exploration and expanding the depth of form finding. Both of the existing sites provide the similar geometric hexagonal/pentagonal shapes, thus providing the starting point of the chosen geometry. The geometry of study is hexagon to start with the base of understanding the design language of the model form.

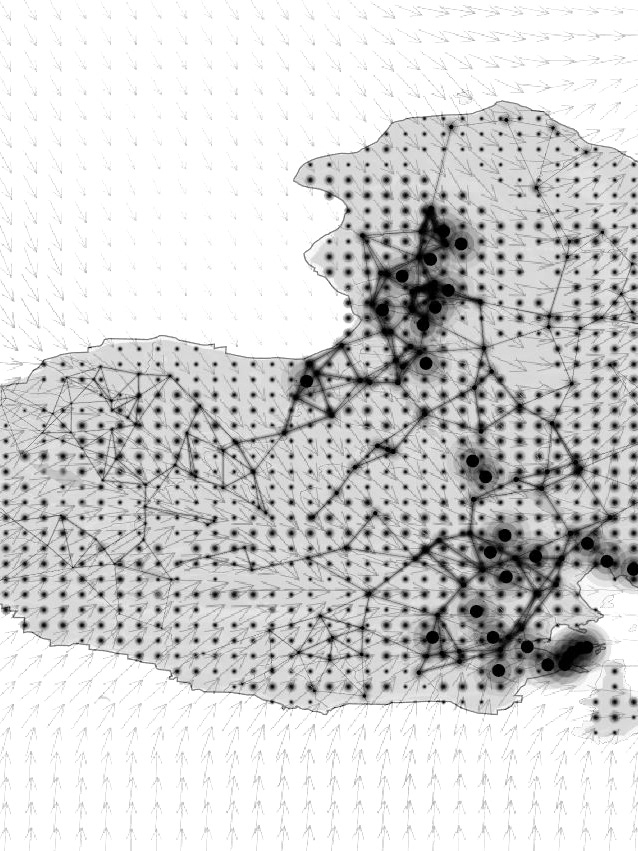
   With the script that is created, the pre-made tool can be reused on any existing site as a case study. In this case, the case study is seven sisters, located in Eastbourne of the United Kingdom. The first step is to gather data from an existing site, as shown in the diagrams on the right. The diagrams study the topologic form and geographic context.
   The Seven Sisters site has unique attributes of chalk like sediments, providing the beaches to be fine. Every year the cliffs erodes approximately 30 to 40 centimeters. The site is provided as a base to allow superimposed forms over the existing site. The forms allow a quick study of form finding. Regardless of the context, the forms are generated to provide the exploration of how python scripting can be practiced and applied onto any site. The python scripting is utilised to show the power of the tool as a way to aesthetically show the compelling land forms generated.
   Furthermore, the Seven Sisters site provides the intricacy of the generated land forms. It is interesting to see how the python scripting is influenced by the different type of surfaces provided and becomes a part of the parameter of the model generated. To expand the tools capabilities, the Seven Sisters model is used the template, reiterating the python script numerous times without compromising the land form of the original Seven Sisters. The model becomes the test and simulation as the test site. The python script act as the tool to continuously generate many shapes and land forms.
   This allows the land form to be studied in the conceptual level and study of form finding. The time saving of scripting provides the extrapolation of generated form. The time saving of generate multiple models provides the precision, accuracy, and efficiency of form finding.

One attractor + dist/100 = high vertical influence + very low curve bends
Two attractor + dist/100 = medium high vertical influence + very low curve bends
Three attractor + dist/100 = medium vertical influence + very low curve bends
Four attractor + dist/100 = low vertical influence + very low curve bends

One attractor + [v[0]+dist/5,v[1]+dist/5,v[2]+100] = high vertical influence + medium curve bends
Two attractor + [v[0]+dist/5,v[1]+dist/5,v[2]+100] = medium high vertical influence + medium curve bends
Three attractor + [v[0]+dist/5,v[1]+dist/5,v[2]+100] = medium vertical influence + medium curve bends
Four attractor + [v[0]+dist/5,v[1]+dist/5,v[2]+100] = low vertical influence + medium curve bends

One attractor + [v[0]+dist/30,v[1]+dist/30,v[2]+300] = high vertical influence + low curve bends
Two attractor + [v[0]+dist/30,v[1]+dist/30,v[2]+300] = medium high vertical influence + low curve bends
Three attractor + [v[0]+dist/30,v[1]+dist/30,v[2]+300] = medium vertical influence + low curve bends
Four attractor + [v[0]+dist/30,v[1]+dist/30,v[2]+300] = low vertical influence + low curve bends

One attractor + [sin(v[0]),cos(v[1]),v[2]+dist] = high vertical influence + high curve bends
Two attractor + [sin(v[0]),cos(v[1]),v[2]+dist] = medium high vertical influence + high curve bends
Three attractor + [sin(v[0]),cos(v[1]),v[2]+dist]= medium vertical influence + high curve bends
Four attractor + [sin(v[0]),cos(v[1]),v[2]+dist] = low vertical influence + high curve bends

import rhinoscriptsyntax as rs
import math
import random

rs.EnableRedraw(False)

srf = rs.GetObject(‘surface’,8)
cntrPoint = rs.SurfaceAreaCentroid(srf)
hexGridCenter0 = rs.AddPoint(cntrPoint[0])
hexGridCenter = rs.PointCoordinates(hexGridCenter0)
hexGridExtend = 100 #rs.GetInteger(“Enter the number of radial levels”, 30, 2)
hexGridClSize = 20 #rs.GetReal(“Edge size of hexagons”, 10.0)
hexGridCAngle = 0
edges = 6
hexGrid = []
pythagoras = 2 * math.sqrt((hexGridClSize * hexGridClSize) - ((hexGridClSize / 2) * (hexGridClSize / 2)))
h = 125 #Z value
n= 200
z= 200
attPoint = ([hexGridCenter[0]+n,hexGridCenter[1]+n,z],[hexGridCenter[0]-n,hexGridCenter[1]-n,z],[hexGridCenter[0]+n*2,hexGridCenter[1]-n,z/10],[hexGridCenter[0]-n*2,hexGridCenter[1]+n,z])
rs.AddPoints(attPoint)

def polygon(center,edges,size,angle):
   tempCircle = rs.AddCircle(center, size)
   tempPoints = rs.DivideCurve(tempCircle, edges, create_points=False, return_points=True)
   tempPoints.append(tempPoints[0])
   tempHexago = rs.AddPolyline(tempPoints)
   tempReturn = rs.RotateObject(tempHexago, center, angle, axis=None, copy=False)
   rs.DeleteObject(tempCircle)
   return tempReturn

for i in range(0, hexGridExtend):
tempSize = pythagoras * (i + 1)
dut = polygon(hexGridCenter, edges, tempSize, 30 + hexGridCAngle)
temp = rs.DivideCurve(dut, (i+1) * edges, create_points=False, return_points=True)
rs.DeleteObject(dut)
hexGrid.extend(temp)

hexGridProj= rs.ProjectPointToSurface(hexGrid,srf,(0,0,-1))

for i in range(0, len(hexGrid)):

pts= rs.AddPoint(hexGridProj[i])
poli1= polygon(pts,edges,hexGridClSize,hexGridCAngle)
surface = rs.AddPlanarSrf(poli1)#hex surface

index = rs.PointArrayClosestPoint(attPoint,hexGridProj[i])
closestpt = attPoint [index]
#print index
dist = rs.Distance(hexGridProj[i],closestpt)
#dist = rs.Distance(hexGridProj[i],attPoint)

surfacecp = rs.SurfaceClosestPoint(surface, hexGridProj[i])
surfacenormal = rs.SurfaceNormal(surface, surfacecp)
vectornew0 = rs.VectorAdd(hexGridProj[i],surfacenormal)
vectornew = [vectornew0[0]+dist/5,vectornew0[1]+dist/5,vectornew0[2]+100]
vec = 0,0,h
#Vector
newPts = rs.MoveObjects(pts,vec) #New points moved z-axis
pts2 = rs.PointCoordinates(newPts)
#rs.AddPoints(newPts)
dist2 = rs.Distance(hexGridProj[i],pts2)

#dist = rs.Distance(attPoint,pts)
#if dist<100 and dist>0:
#vector = rs.VectorCreate(hexGrid[i],attPoint)
line = rs.AddCurve([hexGridProj[i],[pts2[0],pts2[1],pts2[2]*(dist/100)]],3)
obj = rs.ExtrudeSurface(surface,line,True)
#rs.ObjectColor(obj,((random.uniform(0,255)),(random.uniform(0,255)),(random.uniform(0,255))))

rs.DeleteObject(line)
rs.DeleteObject(pts)
rs.DeleteObject(surface)
rs.DeleteObject(poli1)

rs.EnableRedraw(True)

You may also like